How Models Work

We’ll start with a model called Decision Tree. There are fancier models that give more accurate predictions. But desision trees are easy to understand, and they are the basic building block for some of the best models in data science.

For simplicity, we’ll start with the simplest possible decision tree.

1
2
3
4
5
6
7
8
9
10
    Sample Decision Tree
    
        ----------------------------------------
        | Does house have more than 2 bedrooms |
        ----------------------------------------
    / no                                       \ yes
--------------------                 --------------------
| Predicted Price: |                 | Predicted Price: |
| $178000          |                 | $188000          |
--------------------                 --------------------

It divides houses into only two categories. The predicted price for any house under consideration is the historical average price of houses in the same category.

We use data to decide how to break the houses into two groups, and then again to determine the predicted price in each group. This step of capturing patterns from data is called fitting or training the model. The data used to fit the model is called the training data.

The details of how the model is fit(e.g. how to split up the data) is complex enough that we will save it for later. After the model has been fit, you can apply it to new data to predict prices of additional homes.

Improving the Decision Tree

Which of the following two decision trees is more likely to result from fitting the real estate training data?

1
2
3
4
5
6
7
8
9
10
          1st Decision Tree                              2nd Decision Tree
        ------------------------                       ------------------------
        | Does house have more |                       | Does house have more |
        | than 2 bedrooms      |                       | than 2 bedrooms      |
        ------------------------                       ------------------------
     / no                     \ yes                    / no                    \ yes
--------------------      --------------------    --------------------    --------------------
| Predicted Price: |      | Predicted Price: |    | Predicted Price: |    | Predicted Price: |
| $178000          |      | $188000          |    | $188000          |    | %178000          |
--------------------      --------------------    --------------------    --------------------

The descision tree on the left(Decision Tree 1) probably makes more sense. The biggest shortcoming of this model is that it doesn’t capture most factors affecting home price, like number of bathrooms, lot size, location, etc.

You can capture more factors using a tree that has more “splits”. These are called “deeper” trees. A decision tree that also considers the total size of each house’s lot might look like this:

1
2
3
4
5
6
7
8
9
10
11
12
                           ----------------------------------------
                           | Does house have more than 2 bedrooms |
                           ----------------------------------------
                           / no                                   \ yes
       -----------------------------------------      ------------------------------------------
       | Lot size larger than 8500 square feet |      | Lot size larger than 11500 square feet |
       -----------------------------------------      ------------------------------------------
           / no                      \ yes                      / no               \ yes
--------------------        --------------------      --------------------        --------------------
| Predicted Price: |        | Predicted Price: |      | Predicted Price: |        | Predicted Price: |
| $146000          |        | $188000          |      | $170000          |        | $233000          |
--------------------        --------------------      --------------------        --------------------

Your First Machine Learning Model

Selecting Data for Modeling

1
2
3
4
5
6
7
8
9
import pandas as pd

data = pd.read_csv("file_path", index_col=0)

# get all column names
data.columns

# drop missing values (think of na as "not available")
data = data.dropna(axis=0)

Selecting The Prediction Target

1
y = data.Price

Choosing “Features”

The columns that are inputted into our model (and later used to make predictions) are called “features”. In our case, those would be the columns used to determine the home price.

For now, we’ll build a model with only a few features. Later on you’ll see how to iterate and compare models built with different features.

We select multiple features by providing a list of column names inside brackets. Each item in that list should be a string(with quotes).

1
2
3
4
features = ["Rooms", "Bathroom", "Landsize", "Lattitude", "Longtitude"]

# by conversion, this data is called X
X = data[features]

Building Your Model

You will use the scikit-learn library to create your models. When coding, this library is written as sklearn, as you will see in the sample code. Scikit-learn is easily the most popular library for modeling the types of data typically stored in DataFrames.

The steps to building and using a model are:

  • Define: What type of model will it be? A Decision Tree? Some other type of model? Some other parameters of the model type are specified too.
  • Fit: Capture patterns from provided data. This is the heart of modeling.
  • Predict: Just what it sounds like.
  • Evaluate: Determine how accurate the model’s predictions are.

Here is an example of defining a decision tree model with scikit-learn and fitting it with the features and target variable.

1
2
3
4
5
6
7
from sklearn.tree import DecisionTreeRegressor

# Define model. Specify a number for random_state to ensure same results each run
model = DecisionTreeRegressor(random_state=1)

# Fit model
model.fix(X, y)

We now have a fitted model that we can use to make predictions.

In practise, you’ll want to make predictions for new houses coming on the market rather than the houses we already have prices for. But we’ll make predictions for the first few rows of the training data to see how the predict function works.

1
2
3
4
print("Making predictions for the following 5 houses:")
print(X.head())
print("The predictions are: ")
print(model.predict(X.head()))

Model Validation

Measure the performance of your model, so you can test and compare alternatives.

What is Model Validation

In most (though not all) applications, the relevant measure of model quality is predictive accuracy. In other words, will the model’s predictions be close to what actually happens.

Many people make a huge mistake when measuring predictive accuracy. They make predictions with their training data and compare those predictions to the target values in the training data. You’ll see the problem with this approach and how to solve it in a moment, but let’s think about how we’d do this first.

There are many metrics for summarizing model quality, but we’ll start with one called Mean Absolute Error MAE. Let’s break down this metric starting with the last word, error.

The prediction error for each house is:

error = actual - predicted

So, if a house cose $150,000 and you predicted it would cost $100,000 the error is $50,000.

With the MAE metric, we take the absolute value of each error. This converts each error to a positive number. We than take the average of those absolute errors. This is our measure of quality. In plain English, it can be said as:

On average, our predictions are off by about X.

To calculate MAE, we first need a model.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import pandas as pd
from sklearn.tree import DecisionTreeRegressor

data = pd.read_csv("file_path")
# filter rows with missing values
filter_data = data.dropna(axis=0)

feature_names = ["col1", "col2", "col3", "col4"]
X = filter_data[feature_names]
y = filter_data["col5"]

model = DecisionTreeRegressor(random_state=1)
model.fit(X, y)

# model.predict(X.head())

Once we have a model, here is how we calculate the mean absolute error:

1
2
3
4
from sklearn.metrics import mean_absolute_error

predicted_value = model.predict(X)
mean_absolute_error(y, predicted_value)

The Problem with “In-Sample” Scores

The measure we just computed can be called an “In-Sample” score. We used a single “sample” of houses for both building the model and evaluating it. Here’s why this is bad.

The most straightforward way to do this is to exclude some data from the model-building process, and then use those to test the model’s accuracy on data it hasn’t seen before. This data is called validation data.

The scikit-learn library has a function train_test_split to break up the data into two pieces. We’ll use some of that data as training data to fit the model, and we’ll use the other data as validation data to calculate mean_absolute_error.

1
2
3
4
5
6
7
8
9
10
11
12
13
from sklearn.model_selection import train_test_split

train_X, val_X, train_y, val_y = train_test_split(X, y, random_state = 0)

# define model
model = DecisionTreeRegressor()
# fit model
model.fit(train_X, train_y)

# get predicted value on validation data
val_predictions = model.predict(val_X)

mean_absolute_error(val_y, val_predictions)

Underfitting and Overfitting

Fine-tune your model for better performance.

Experimenting With Different Models

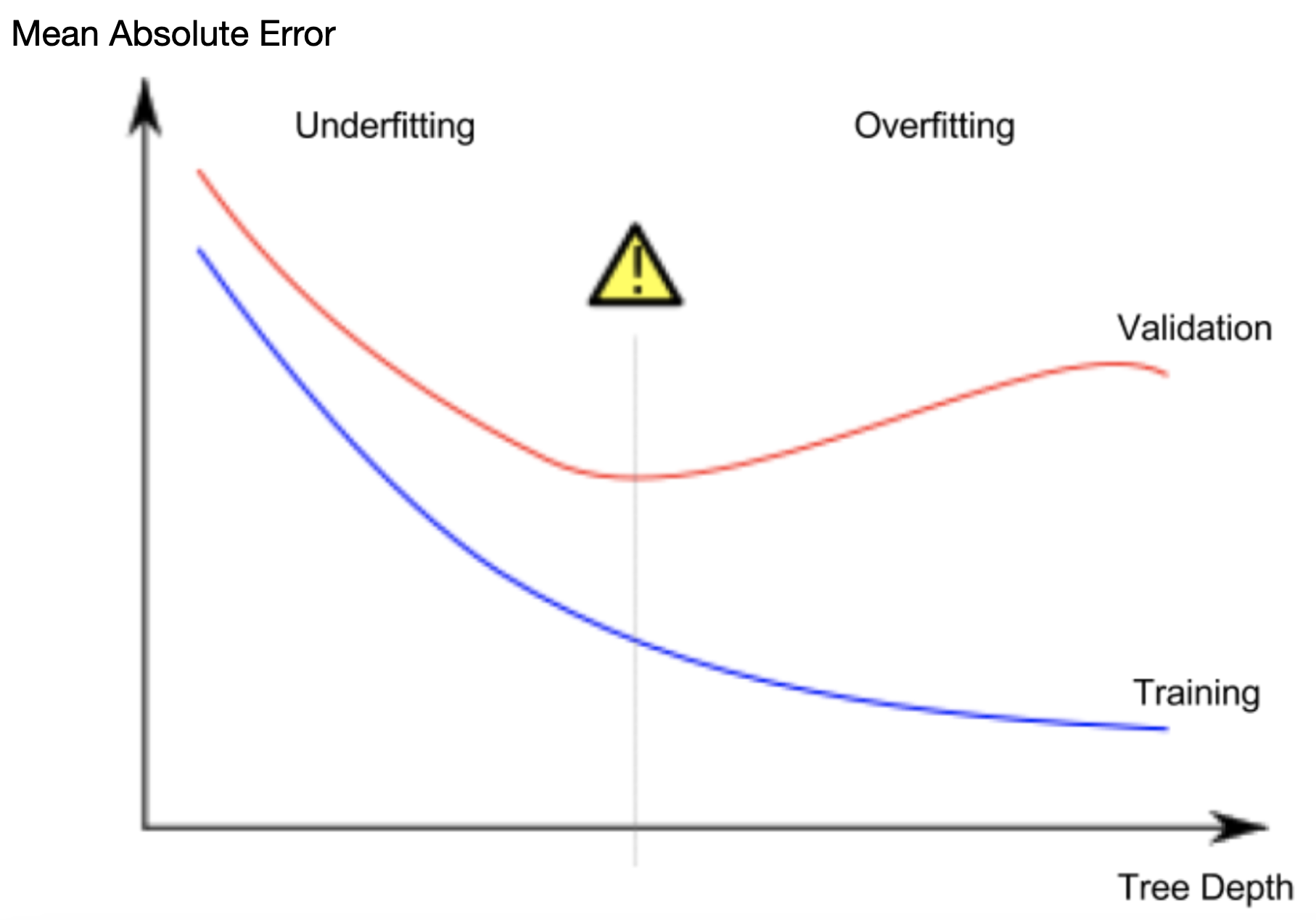
You can see in scikit-learn’s documentation that the decision tree model has many options (more than you’ll want or need for a long time). The most important options determine the tree’s depth. Recall from the first lesson in this course that a tree’s depth is a measure of how many splits it makes before coming to a prediction.

Leaves with very few houses will make predictions that are quite close to those homes’ actual values, but they may make very unreliable predictions for new data (because each prediction is based on only a few houses).

This is a phenomenon called overfitting, where a model matches the training data almost perfectly, but does poorly in validation data and other new data. On the flip side, if we make our tree very shallow, it doesn’t divide up the houses into very distinct groups.

At an extreme, if a tree divides houses into only 2 or 4, each group still has a wide variety of houses. Resulting predictions may be far off for most houses, even in the training data (and it will be bad in validation too for the same reason). When a model fails to capture important distinctions and patterns in the data, so it performs poorly even in training data, that is called underfitting.

Mean Absolute Error

Example

There are a few alternatives for controlling the tree depth, and many allow for some routes through the tree to have greater depth than other routes. But the max_leaf_nodes argument provides a very sensible way to control overfitting vs underfitting. The more leaves we allow the model to make, the more we move from the underfitting area in the above graph to the overfitting area.

We can use a utility function to help compare MAE scores from different values for max_leaf_nodes:

1
2
3
4
5
6
7
8
9
from sklearn.metrics import mean_absolute_error
from sklearn.tree import DecisionTreeRegressor

def get_mae(max_leaf_nodes, train_X, val_X, train_y, val_y):
    model = DecisionTreeRegressor(max_leaf_nodes=max_leaf_nodes, random_state=0)
    model.fit(train_X, train_y)
    val_prediction = model.predict(val_X)
    mae = mean_absolute_error(val_y, val_prediction)
    return mae

The data is loaded into train_X, val_X, train_y, val_y using the code you’ve already seen (and which you’ve already written).

We can use a for-loop to compare the accuracy of models built with different values for max_leaf_nodes:

1
2
3
4
# compare MAE with different max_leaf_nodes
for max_leaf_node in [5, 50, 500, 5000]:
    my_mae = get_mae(max_leaf_node, train_X, val_X, train_y, val_y)
    print(f"Max Leaf Node: {max_leaf_node}\t\t Mean Absolute Error: {my_mae}")

Of the options listed, 500 is the optimal number of leaves.

Random Forests

Using a more sophisticated machine learning algorithm.

Introduction

Decision Tree leaves you with a difficult decision. A deep tree with lots of leaves will overfit because each prediction is coming from historical data from only the few houses at its leaf. But a shallow tree with few leaves will perform poorly because it fails to capture as many distinctions in the raw data.

Even today’s most sophisticated modeling techniques face this tension between underfitting and overfitting. But, many models have clever ideas that can lead to better performance. We’ll look at the random forest as an example.

Example

You’ve already seen the code to load the data a few times. At the end of data-loading, we have the following variables:

  • train_X
  • val_X
  • train_y
  • val_y
1
2
3
4
5
6
7
8
9
10
11
12
import pandas as pd
from sklearn.model_selection import train_test_split

file_path = "file_path"
data = pd.read_csv(file_path)
filtered_data = data.dropna(axis=0)

y = filtered_data["price"]
feature_name = ["col_1", "col_2", "col_3", "col_4"]
X = filtered_data[feature_name]

train_X, val_X, train_y, val_y = train_test_split(X, y, random_state=0)

We build a random forest model similarly to how we built a decision tree in scikit-learn - this time using the RandomForestRegressor class instead of DecisionTreeRegressor.

1
2
3
4
5
6
7
8
9
10
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error

model = RandomForestRegressor(random_state=1)
model.fit(train_X, train_y)

val_preds = model.predict(val_X)
mae = mean_absolute_error(val_y, val_preds)

print(mae)

Conclusion

There is likely room for further improvement, but this is a big improvement over the best decision tree error of 250,000. There are parameters which allow you to change the performance of the Random Forest much as we changed the maximum depth of the single decision tree. But one of the best features of Random Forest models is that they generally work reasonably even without this tuning.

Conclusion

  1. Import Data
  2. Select columns to predict and feature columns
  3. Split Data into training data and validation data
  4. Define the model
  5. Fit model
  6. Use metrics to summarize model quality
  7. Choose the best quality model and training all of the data